たのしい算数⑦ ~入試問題にチャレンジ 面積の問題だけど・・・
こんにちは。教室長の西野です。
少し、久しぶりになってしまいました。
ここ最近は雨の日が続いており、それもかなりひどい雨が降っています。
皆さんのところは大丈夫でしょうか? 避難や被害に遭われた方、本当に大変だと思いますが、頑張ってください。
私は今でも夢を持っています。そう、「気象予報士」になりたいという夢を。
今回の雨の降り方も、天気図的には過去にも同様な状況がありました。では、最近は何が違うのか?
太平洋(日本近海)の水温が高くなっているということです。
これが、多量の水蒸気を含んでしまうことで、多くの雨を降らせる原因となっています。よく「地球温暖化」という言葉を耳にすると思いますが、こういうところでも影響が出ているということです。
梅雨末期の雨はとてもひどくなるので、十分お気を付けください。
では、本論に入ります。今日は図形の面積のお話をしたいと思います。
三角形の面積を求める、これは小学校5年生の履修内容です。
面積を求める「公式」は
(底辺)×(高さ)÷2
これさえ分かれば、答えを出せる!と。では、次の問題にチャレンジしてみましょう。
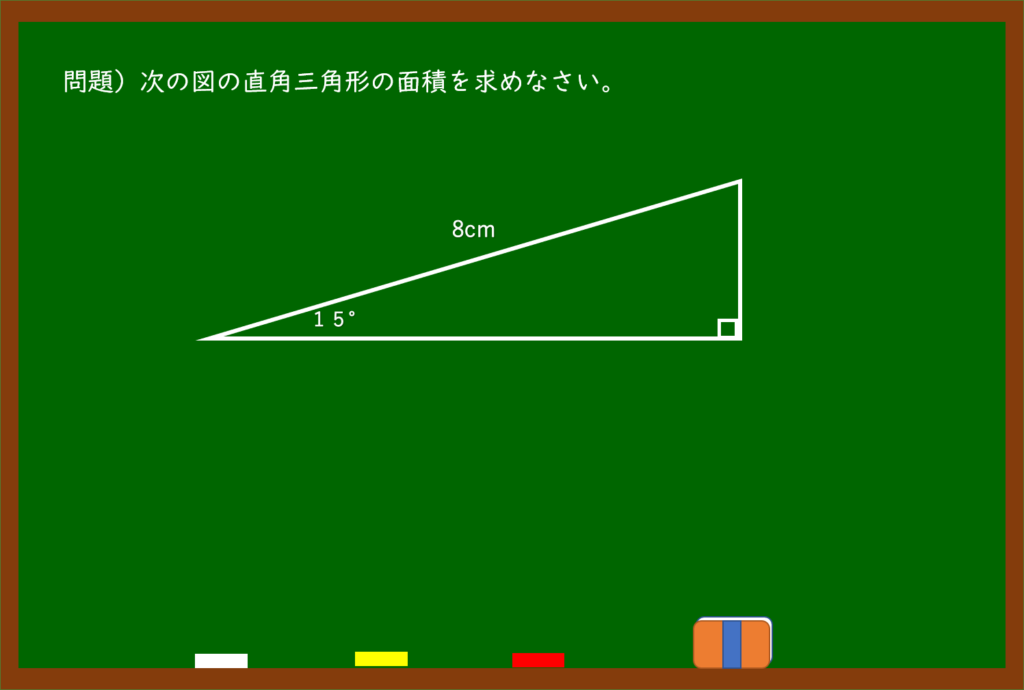
どうですか?
分かっている情報は、
①直角三角形である
②斜辺(直角と向かい合っている辺のこと)
③15°の角がある
ということで、「底辺」、「高さ」の情報はどこにもないですね。
しかし、小学校で習っていることを総動員して考えると・・・・
直角三角形 → 三角定規 (30°・60°・90°/45°・45°・90°)
これがヒントにならないか・・・ 15°を2倍すると30°だ!!
では2つ重ねてみよう・・・というところから思考が始まります。
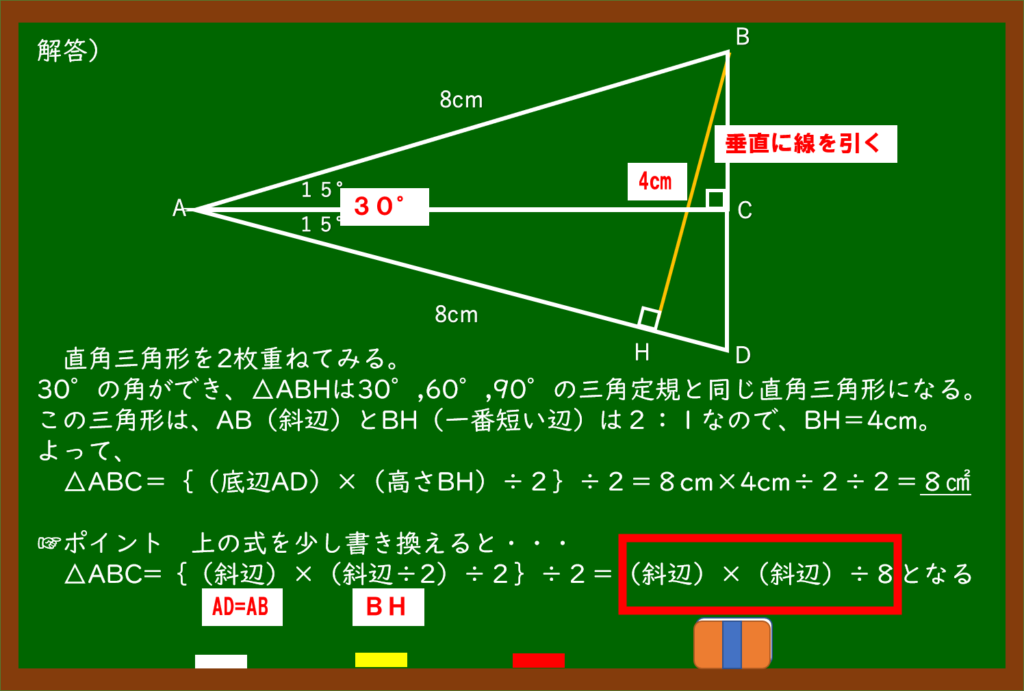
いかがですか?小学校の知識だけで解くことができました。
しかも、15°の直角三角形の面積は
(斜辺)×(斜辺)÷8 で求められるということもわかりました。
「底辺」「高さ」が分からなくても解けるんですね・・・。
これを高校生が解くとすると
底辺=8cos15° 高さ=8sin15° より
S=8cos15° × 8sin15° ÷ 2 =8・8・(1/2)sin 30°・(1/2)
=(1/2)・(1/2)・(1/2)・8・8
=(1/8)・8・8
同じ式になりました! 三角関数・二倍角の公式等を使うと出せますが、小学生の知識でも解けることを考えると、何だがもやもやしますね。
でもこういうことを考えるのが、算数の面白いところです。
私の高校の時の恩師である数学の先生は、「難しい問題を難しい公式や難しい知識で解く必要はない、いかに簡単な知識で解けるかを考えることが、必要なんだよ。」微分・積分の授業の時に、いつも高1程度の数学Ⅰの知識での解法を授業中に紹介してくれました。普通に授業中に拍手が起こる不思議な授業でした。
何年か前のセンター試験の数学の問題も、中学数学程度で解ける問題が、ありましたが、実はその問題がその年の数学の平均点を大きく下げる問題となったというのは正直驚きでしたが・・・
算数は、やはり奥深いです。
それではまた。






