みなさんこんにちは。教室長の西野です。

2020年も後半に入っているのですが、なかなかコロナ呪縛からとけなく、いかにしてコロナと共存していくか、などという言葉も出てくるくらい、通常には戻れてないですね。もう半月もすれば、「入試」の風が少しずつ吹いてくると思うのですが・・・来年の事を考えると心配ですが、どんなことになっても準備だけはしっかりしていないとダメですよね。

さて、今日は正多角形のお話をします。

まず、正多面体は５つしか存在しないのはご存知ですか？

正四面体・正六面体（立方体）・正八面体・正十二面体・正二十面体

の５つです。他は存在しません。

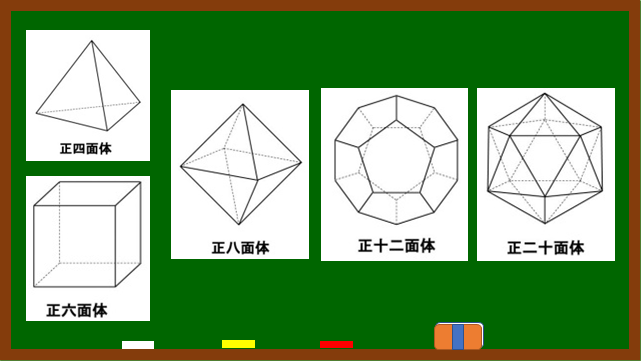
理由は２つあります。

➀　正多角形が3枚以上ないと立体の頂点（角：かど）が作れない。

➁　頂点（角：かど）に集まる正多角形の角度の合計は360度未満でないといけない。
これを考えると、正六角形で正多面体を作ることができません。３枚集まると、集まったところの角度が３６０°になってしまい、ぺったんこになってしまうからです。

また、正三角形、正方形、正五角形の場合は、それぞれ、正四面体・正八面体・正二十面体／正六面体（立方体）／正十二面体が存在できますが、➀，②の理由からこの５つしか存在できません。

正多面体であるから、とても形がきれいですね。

空間から平面に話を移しましょう。

私は正六角形が大好きです。なぜか？それはよくわかりません。ただ、とてもきれいな図形に見えてしまうわけです。今日はその正六角形の入試問題を見てみましょう。

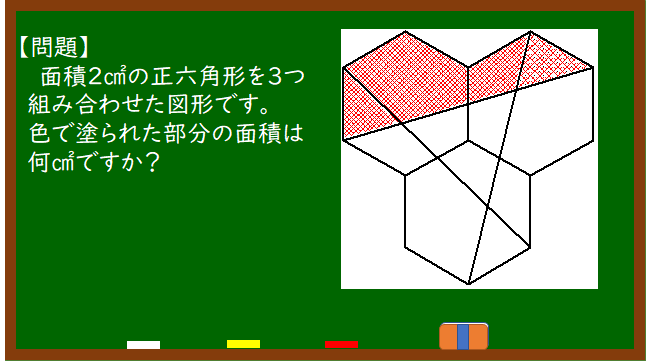
ある私立中学の入試問題（改題）です。

答えは・・・２㎠です。気づいた人も多いと思いますが、右側の四角形の部分を左の五角形の下に移動させると、ちょうど正六角形１個分になりますので、答えは２㎠となります。

なんだ、と思うかもしれませんが、正六角形はこのように意外と？簡単に答えが出たりします。これは正六角形の対角線を引くと正三角形が出てきたり、出てくる角度が６０°、１２０°だったりとヒントの宝庫だったりします。感覚？と思うかもしれませんが、図形の問題に当たっていくと、正六角形の問題にたくさん当たります。意外と悩む問題が多かったりします。でも、ヒントばかりの図形ですから、逃げずに考えてみましょう。

★立方体を切断する時に出てくる「正六角形」

★高校数学Bで、ベクトル表示をするときに必ず出てくる「正六角形」

いかがですか？図形が嫌いな方・・・接する回数が増えてくると案外楽しいものですよ。

今日は色んな話を並べました。好きなものは色々言いたくなりますが、今日はこの辺で。またお会いしましょう。